More Special Right Triangles

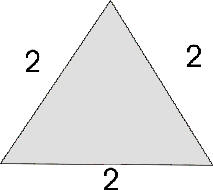
     <== an equilateral triangle

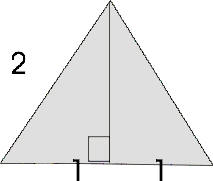<== an equilateral triangle split into two equal triangles.  These are called 30˚-60˚ right triangles.  Why?  Well, an equilateral triangle has all angles equal to 60˚.  When we put the height in, it split the top angle in half, into two 30˚ angles.  So, in one of the right triangles, there is a 90˚ angle, a 60˚ angle, and a 30˚ angle.

Now let's say we want to find the height of the equilateral triangle (the side b of the small right triangle).  First use the Pythagorean Theorem.

a² + b² = c²
b² = c² - a²

b^{2 =} 2² - 1²
b² = 4 - 1
b² = 3
b = √3 or 1√3

Let's try it again if the side length of the equilateral triangle is 4.

b² = c² - a²

b² = 4² - 2²
b² = 16 - 4
b² = 12
b = √12 = 2√3

Notice a pattern? :) ... if you don't, the rule is below:

***************************

In a 30˚-60˚ right triangle, if the smallest side is a units, then the hypotenuse will be 2a units, and the longer side will be a√3 units.

Similarly, if the side length of an equilateral triangle is a units, then the height will be ½a√3 units.

***************************

Click here to go back to the first page of special right triangles.
Click here to go back to the index.