Special Right Triangles

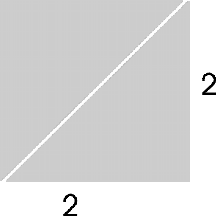
Say we have a figure like this...

Each of the two triangles that make up the square have equal lengths of the legs (because all sides of a square are equal).  They also each have a 90 degree angle and two 45 degree angles (which goes along with the fact that the legs are equal).  Because of these two facts, we call this triangle an isosceles right triangle or a 45˚ right triangle.  If we wanted to find the hypotenuse, we could use the Pythagorean Theorem...

a² + b² = c²
2² + 2² = c²
4 + 4 = c²
8 = c²
c = √8 = 2√2

Ok...now say the legs are each 1...

1² + 1² = c²
1 + 1 = c²
2 = c²
c = √2 or 1√2

Now look for a pattern....

***********************

Ok...if you haven't found it, I will just give you the rule:

In an isosceles right triangle, if the legs have length a, then the hypotenuse will have a length of a√2.

You often can use this when trying to find the diagonals of a square.

***********************

Click here to go to the next page of special right triangles.
Click here to go back to the index.