More Graphing Parabolas

Alright.  If you remember how to find the vertex of a quadratic equation, find it for this one:

y = 3x² + 12x + 7

-b/2a = -12/2(3) = -12/6 = -2
3(-2)² + 12(-2) + 7 =
3(4) - 24 + 7 =
12 - 17 = -5
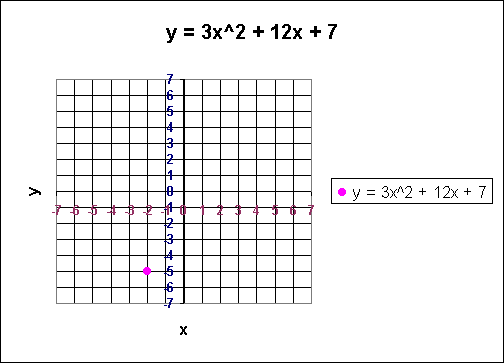
vertex: (-2, -5)

Let's set up some axes and put on the vertex.

Now I want you all to pretend there is a line running vertically, with the x-coordinate of the vertex (in this case, the line would be the equation x = -2).  This is your line of symmetry for the parabola.  If you have a point, with (x, y) coordinates, the other x-coordinate for that same value of y will be the same distance from the line as the first x, but on the other side.  As an example, let's make a table of values.

x       |    y
-2     |   -5
0, ?   |   ?

3(0)² + 12(0) + 7 = 7

x       |    y
-2     |   -5
0, ?   |   7

0 (x₁) is 2 units to the right of the line of symmetry.  To get the other x-coordinate, we find what is 2 units to the left of the line of symmetry.
-2 - 2 = -4

x       |    y
-2     |   -5
0, -4 |   7

Now find some more...

x       |    y
-2     |   -5
0, -4 |   7
-1, ? |   ?

3(-1)² + 12(-1) + 7 =
3(1) - 12 + 7 =
3 - 5 = -2

x       |    y
-2     |   -5
0, -4 |   7
-1, ? |  -2

-1 is 1 unit to the right of the line of symmetry.  What is 1 unit to the left? -2 - 1 = -3

x       |    y
-2     |   -5
0, -4 |   7
-1, -3|  -2

Now that we have a few more points, let's graph them, and then connect the points with a smooth curve:

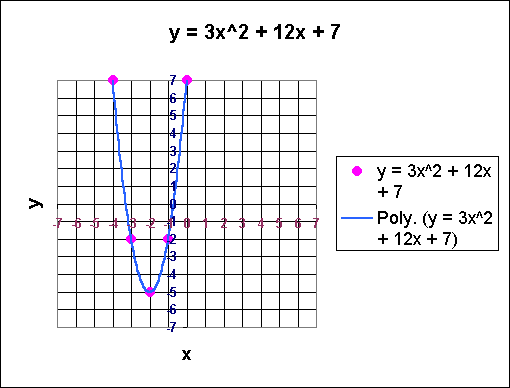
Of course, since I am computer-graph challenged, I could not include the arrows that should be at the top of the graph (the two upper points of the U), showing that the solutions are infinite.

~*~*~*~*~*~*~*~*~*~*~*~*~*~*~*~*~*~*~*~*~*~*~*~

We will do one more, and then I will leave you some equations to do, and their solutions without the explanations.

Here is our equation: y = -3x² + 3x - 1

Find the vertex...
x = -b/2a = -3/2(-3) = -3/-6 = 1/2
y = -3(1/2)² + 3(1/2) - 1 = -3(1/4) + 3/2 - 2/2 = -3/4 + 6/4 - 4/4 = -1/4
vertex: (1/2, -1/4)

Make a table of values...
x        |        y  
1/2    |  -1/4
1, ?    |   ?
-3(1)² + 3(1) - 1 = -3(1) + 3 - 1 = -1
1 is 1/2 units to the right of 1/2.  What is 1/2 units to the left? 0
x        |        y  
1/2    |  -1/4
1, 0   |   -1
-1, ?  |    ?
-3(-1)² + 3(-1) - 1 = -3(1) - 3 - 1 = -7
-1 is 3/2 units to the left of 1/2.  What is 3/2 units to the right? 2
x        |        y  
1/2    |  -1/4
1, 0   |   -1
-1, 2  |  -7

Now I suppose you could graph these, although it might be better to get more points.  Here is the graph:

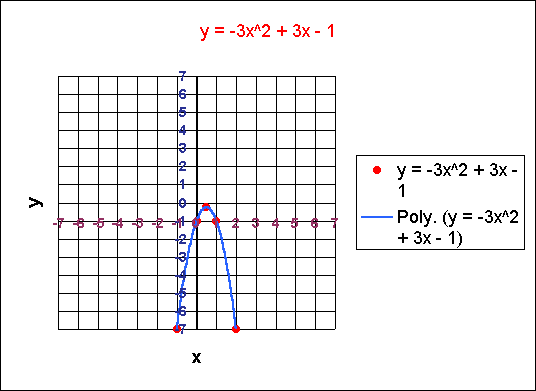
Again, there should be arrows at the bottom, indicating infinite solutions.

Here are some more to graph.  Your points obviously don't have to match, but your parabola has to basically look the same:
1) y = -x² + 2x + 5
2) y = 4x² - 2x + 3
3) y = x² - 4

Answers

Click here to go back to the first page of graphing parabolas.
Click here to go to sketching parabolas.
Click here to go back to the index.