Solving Systems of Equations
(with graphs)

Alright everyone, now that we have mastered some basics, we can go on to other topics.

system of equations: two or more equations using the same variables

For example a system of equations would be:
x + y = 4 and 2x + y = 7

There are three possible things that the lines for these equations could do when graphed:

intersect: meet (cross) at one point - this means there is one solution to the system of equation, and it is called the simultaneous solution.  It is where the lines cross. e.g. x + y = 4, 2x + y = 7

coincide: basically lie on top of each other - have all the same points that make it true - this means there are infinitely many simultaneous solutions to the system of equations. e.g. x + y = 4, 2x + 2y = 8

parallel: the lines never meet/cross (but are on the same graph) - this means there are no simultaneous solutions (no points are solutions of both equations). e.g. x + y = 4, x + y = 5

Let's graph these examples.

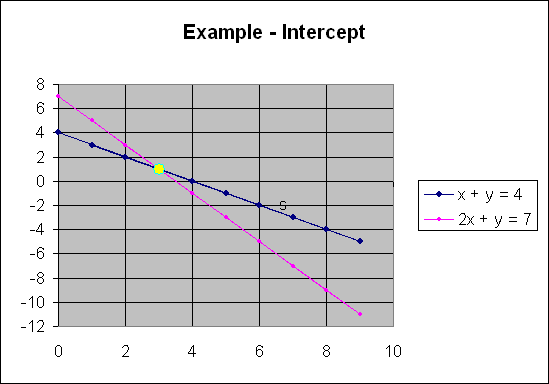
As you can see (or maybe you can't, but it's still true), the lines cross at (3,1), which means the simultaneous solution is (3,1).  Basically that means that when x = 3 and y = 1, both equations are true.  You can substitute to prove this.
x + y = 4, 3 + 1 = 4 YES
2x + y = 7, 2(3) + 1 = 7, 6 + 1 = 7 YES

 

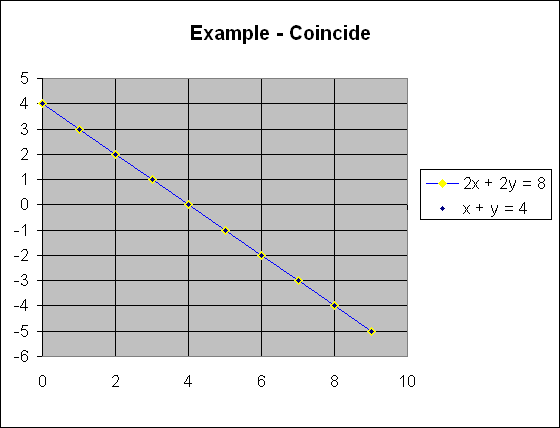
This one is harder to see, but the lines are supposed to be in the same space.  All the points are shared.  Any point on the line will satisfy both equations. Let's pick one and check: (4,0), x = 4, y = 0
2x + 2y = 8, 2(4) + 2(0) = 8, 8 = 8 YES
x + y = 4, 4 + 0 = 4 YES

 

 

 

 

 

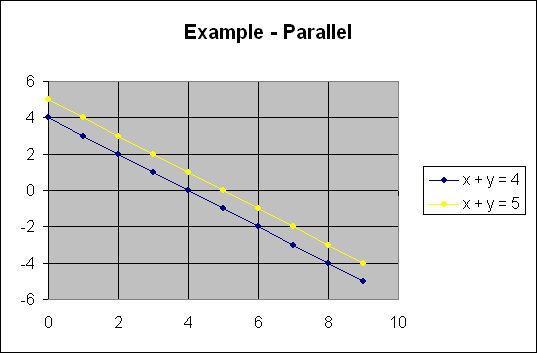
This is pretty easy to see.  The lines are parallel.  They do not have ANY simultaneous solutions.  No points on either line will satisfy both equations.  Let's try one to check: (2, 2), x = 2, y = 2
x + y = 4, 2 + 2 = 4 YES
x + y = 5, 2 + 2 ≠ 5 NO

 

 

 

 

Click here to go back to the index.