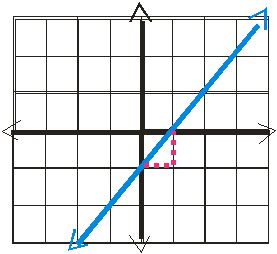
 As you can see, the line crosses
the y-axis at (0,-1), so the y-intercept is -1.
As you can see, the line crosses
the y-axis at (0,-1), so the y-intercept is -1.More Slope
More slope...well...there is more...
BIG RULE: PARALLEL LINES HAVE THE SAME SLOPE
PERPENDICULAR LINES HAVE NEGATIVE RECIPROCAL OF THE OTHER'S SLOPE
ALSO BIG RULE: Horizontal lines have 0 slope, because the change in y will be 0, and whatever the change in x is, 0 divided anything is 0.
Vertical lines have undefined slopes, because the change in x will be 0, and whatever the change in y is, anything divided by 0 is undefined.
Now for a vocabulary word...
y-intercept: y coordinate when the line crosses the y-axis (when x = 0)...commonly denoted using "b"
For example, let us make the graph of x - y = 1
x - y = 1
-y = 1 - x
(-1)-y = (-1)1 + (-1)-x
y = x - 1
x | y
0 | -1
1 | 0
2 | 1
 As you can see, the line crosses
the y-axis at (0,-1), so the y-intercept is -1.
As you can see, the line crosses
the y-axis at (0,-1), so the y-intercept is -1.
*********
BIG EQUATION::::::
y = mx + b
in which m is the slope of the line and b is the y-intercept
So...we had changed x - y = 1 to slope equation form where it was y = x - 1
if there is no coefficient on x, it is a 1, so using that form, m = 1 and b = -1
We already graphed it, so we know this is true (check the slope if you don't believe me *_*)
Now...we didn't even have to make a table of values if we knew this. We would just make a point at (0,-1) because we know that is the y-intercept. Then we would use the slope to make another point. We'd go 1 to the right and 1 up, or 1 to the left and 1 down, or 2 to the right and 2 down, etc. In any way, it will give another point on the line. If you want a third point, just do it again, and connect the points.
Click here to go back to the first slope page.
Click here to go back to the index.