Intercepts
Intercept: where a line crosses an axis
On normal graphs, we have the x and y intercepts. As one might guess, the x-intercept is where a graphed line crosses the x-axis and the y-intercept is where it crosses the y-axis.
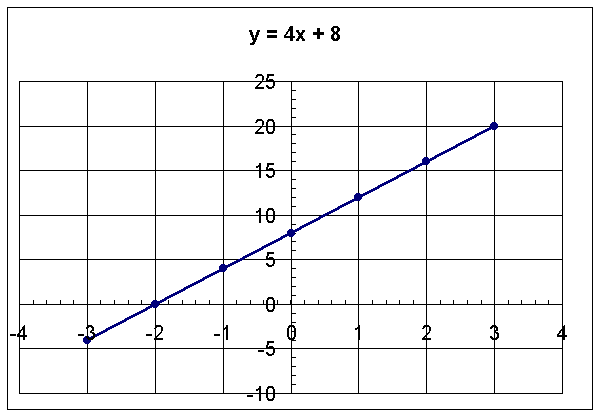
The graph below is a graph of the equation y = 4x + 8.

(There should be arrows on both ends, but as always, I am excel drawing challenged.) If you cannot see, the line crosses the x-axis at point (-2,0) and the y-axis as (0,8).
An intercept is the point in which the other axis' coordinate is
equal to 0.
So the x-intercept is the point when y = 0, and the y-intercept is the point
when x = 0.
Therefore, you can find them without using a graph, just a table
of values. Find the x and y-intercepts of the equation:
5x + 2y = 6
| x | y |
| 0 | 3 |
| 6/5 | 0 |
The x-intercept is 6/5 and the y-intercept is 3.
Intercepts come in handy when doing other things with graphs, such as using slope.
Some equations do not have both x and y-intercepts. These equations can be linear, quadratic, etc. I will show a linear equation (in quadratics, an equation had no x-intercepts if solving it when y = 0 gives you imaginary solutions).
x = 4
Ok. Find the x-intercept. When y = 0, x = 4 (still, because x = 4 no
matter what). With that same reasoning, x can never equal 0, because it
always equals 4. Therefore, there is no y-intercept.
If you want, find the x and y-intercepts of the following equations:
1) 2x + 6 = 3y
2) x - 9 = 7y
3) y = 8
Answers
Click here to go back to the index.